Side channel attacks – Attacks on TLS Implementations

22.9.1 Side channel attacks

In side channel attacks, Eve exploits information that the implementation of a cryptographic algorithm leaks through so-called side channels. Side channels are observable physical quantities, such as the execution time of a cryptographic algorithm’s implementation or the instantaneous power consumption or electromagnetic emanations of a cryptographic circuit, that depend on the intermediate values processed by the implementation of that cryptographic algorithm. Figure 22.3 gives an overview of side channels known to leak data-dependent information.

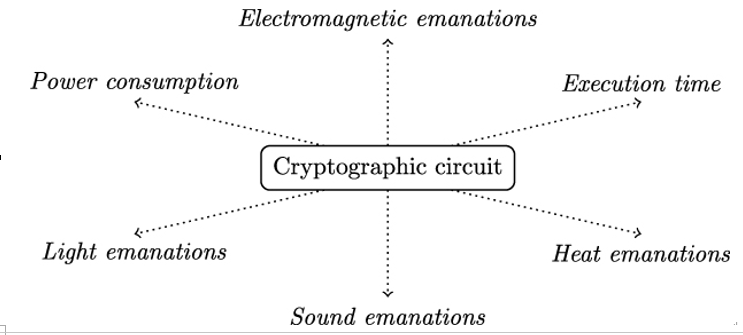
Figure 22.3: Various side channels leaking information about the intermediate values processed by the implementation of a cryptographic algorithm

As an example, Algorithm 11 shows a naive implementation of the square-and-multiply algorithm. The algorithm is often used to compute the modular exponentiation operation in the RSA public-key-encryption scheme (see also Chapter 7, Public-Key Cryptography) because it reduces the number of multiplications required by exploiting binary representation of the exponent. However, unfortunately for Alice and Bob, the naive implementation in Algorithm 11 has a timing side channel.

The multiplication b ← A⋅b (mod n) in the loop iteration i is calculated only if the corresponding bit ki in the exponent is 1 and is omitted otherwise. As a result, if Eve can precisely measure the execution time of each loop iteration, she can determine the secret bits of the RSA exponent. The data-dependent execution time variation therefore constitutes the so-called side channel leakage.

  Algorithm 11: The Square–and–multiply algorithm [117].

Require: a ∈ ℤn, integer 0 < k < n whose binary representation is k = ∑ i=0tki2i
 Ensure: ak (mod n)
 b ← 1
 if k = 0 then
 return b
 end if
 A ← a
 if k0 = 1 then
 b ← a
 end if
 for i in 1 to t do
 A ← A2 (mod n)
 if ki = 1 then
 b ← A · b (mod n)
 end if
 end for
 return b

In general, a side channel leakage is the measured variation of the observed physical quantity, for example, execution time or instantaneous power consumption, during the execution of a cryptographic algorithm. As an example, Figure 22.4 shows the instantaneous power consumption of an AES circuit for different Hamming distance values – the number of bits at which two consecutive values differ – for intermediate data processed by AES.

The power consumption in Figure 22.4 around sample #45 is equivalent to the Hamming distance between the current value of an intermediate register and the result of the SubBytes operation that overwrites the current value.

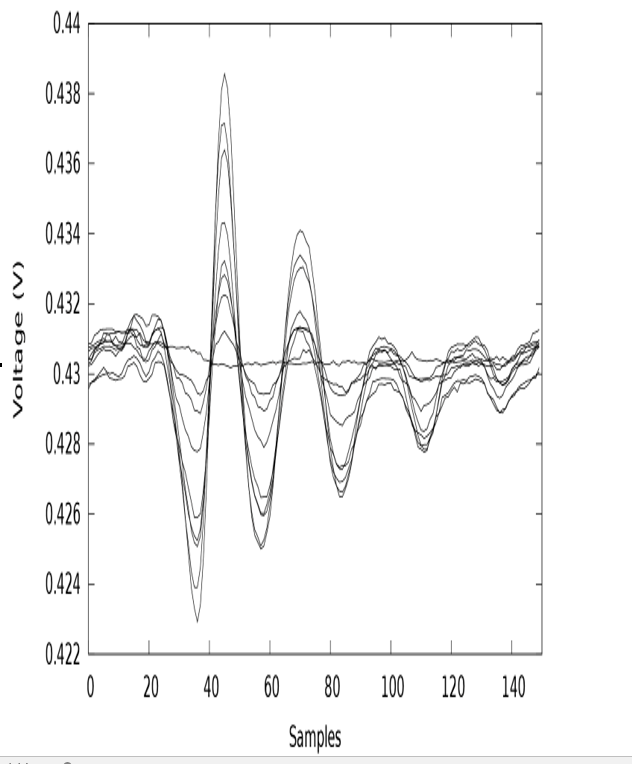
Figure 22.4: Power consumption of an AES hardware implementation when the output of the SubBytes operation is stored in an intermediate register

This is because in CMOS technology, the power consumption of storing a value in a register is proportional to the number of bit flips in that register when the old value is overwritten with the new one.